
Your desired letter will now be entered as a capital letter. To use a capital letter, press shift then alpha. For example, if you would like column Y1 to be filled with the values of X1 divided by 2, write X1/2 in the editing field at the bottom of the screen.
To change a value, highlight the desired cell and enter a new value with the numerical keys.

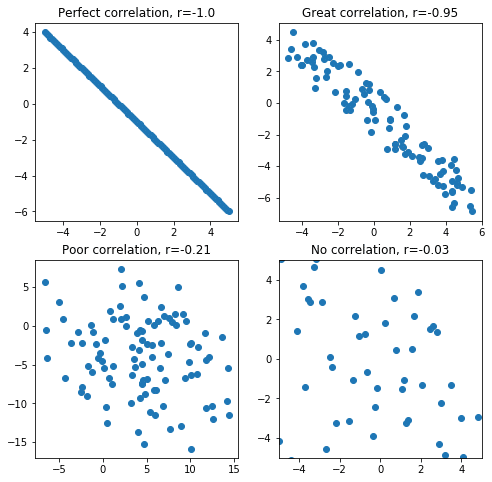
Highlight the cell that you wish to clear.Using the Data tab Clearing an element from a data table You will see the table of statistical values. Highlight the Stats tab at the top of the screen.Once you have entered your data into the table in the Data tab, you may view the statistical values: mean, standard deviation, median, etc. When the model is select, the bottom banner will include the predicted value and the equation. You can now use the down/ up keys to move from a data point to the regression model. Highlight the model you would like to use.While on the Graph tab, press the ok key to view a list of regression model options.Once you have created a scatterplot, you may plot a regression model. The coordinates of the selected point will be displayed in the bottom banner along with the correlation coefficent, r. You will see the points that represent your data. Highlight the Graph tab at the top of the screen.Once you have entered your data into the table, you may view a scatterplot of your data. In the second column (Y1), enter the values of the second variable of your data set.In the first column (X1), enter the values of the first variable of your data set.When you enter the Regression app, you must enter your data into a two-column table. Getting started Entering your data into the table This application allows you to perform statistical computations on two-dimensional data sets. Press the ok key to enter the application. On the third hand (running out of hands) - you're talking about trends? Is this a temporal problem? If it is, be a little cautious with over interpreting trend lines and statistical significance.To enter the Regression application, highlight the app using the directional keys. For this, use model <- loess(y ~ x, data=dataset, span=.), where the span variable controls the degree of smoothing. Loess is just like that but uses regression instead of a straight average.

It's easiest to imagine a "k nearest-neighbour" version, where to calculate the value of the curve at any point, you find the k points nearest to the point of interest, and average them. This does linear regression on a small region, as opposed to the whole dataset. On the other hand, if you've got a line which is "wobbly" and you don't know why it's wobbly, then a good starting point would probably be locally weighted regression, or loess in R.
OVERLAY A QUADRATIC AND LINEAR SCATTER PLOT HOW TO
There's a lot of documentation on how to get various non-linearities into the regression model. So you might want to try polynomial regression in this case, and (in R) you could do something like model <- lm(d ~ poly(v,2),data=dataset). For instance, if you're trying to do regression on the distance for a car to stop with sudden braking vs the speed of the car, physics tells us that the energy of the vehicle is proportional to the square of the velocity - not the velocity itself. Please, if I'm making bad assumptions then ignore my answer.įirst, it's possible that your data describe some process which you reasonably believe is non-linear. It would help a lot if you could put up a scatterplot and describe the data a bit. Your question is a bit vague, so I'm going to make some assumptions about what your problem is.


 0 kommentar(er)
0 kommentar(er)
